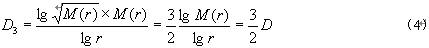PP/PS多相聚合物相形態演變及其機理研究
時間:2005-10-14
李云巖 盛京*
(天津大學材料科學與工程學院 天津 300072) *
shengxu@public.tpt.tj.cn
† National Nature Science Foundation of China(Grant No.50390094)
本文研究了聚丙烯/聚苯乙烯共混過程中相發展過程,討論了分散相顆粒尺寸及其分布的變化規律,以分散相脆性破裂理論為基礎,建立了分形維數的數學模型,通過比較該理論模型結果與試驗結果,證明了共混中分散相破碎具有脆性破碎的特征。
若混煉過程中分散相破碎具有脆性破碎的特征, 則分散相顆粒尺寸變化滿足[1]:
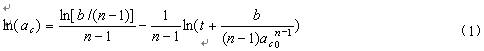
a
c0為初始時刻的顆粒尺寸,t為混煉時間。式(1)描述了分散相顆粒的粒徑與時間的關系,暫稱為”分散理論”,其中n和b成為分散系數。可建立分散相破碎的理想模型 (圖1) 。

在二值化SEM圖像上創建不同邊長r的正方形,記錄該正方形中所包含的分散相顆粒數M(r) ,根據分形理論可按式(2)求得分形維數[2]。

在研究自然界中實際分形的時候,首先必須判斷所研究的對象是否確實分形,為此引入標度函數S(L)來研究對象的復雜程度。

若隨著L的變化,S(L)為恒定值,則表示研究對象的復雜程度不隨標尺的變化而變化,即它具有無標度性,或自相似性。通過此種方法求得的是SEM圖像中分散相顆粒分布的分形維數,改值處于0~2范圍內, 基于整個體系具有空間上的自相似性,可根據式(2)推導出分散相顆粒在三維空間分布的分形維數D3。
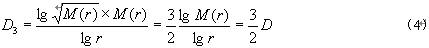
為研究高分子共混中分散相破碎機理, 建立了分散相破碎機理與分形行為關系。若分散相破碎屬脆性破裂, 不妨建立分散相破碎的理想模型,如圖1. 假設分散相顆粒的初始尺寸為ac0,所創建的正方體的最大邊長為rmax, 該正方體包含的顆粒數為M(rmax),則此時的分形維數為:

由于n, b值與加工條件及材料性質有關,這樣就建立了分形維數與加工條件等因素相關的數學模型, 可通過比較分形維數的實驗值和計算值對該模型及斷裂機理進行討論。
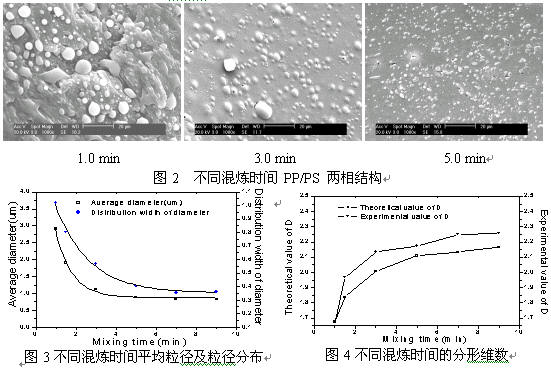
隨著混煉時間的增加,分散相顆粒的粒徑及其分布寬度逐漸減小,分散相的分布具有自相似性,分形維數逐漸增大并在混煉后期穩定下來,分形維數的實驗值與理論值具有一致的變化規律,說明分散相的破裂確有脆性破裂的特征。
參考文獻 [1] 周家敏.多組分多相聚合物共混過程在線分析.天津大學碩士論文,1996,115-116
[2] Takayasu H. Fractals in the physical sciences; Manchester university Press: Manchester and New York, 1990, 11-17
論文來源:2004年全國高分子材料科學與工程研討會論文集