高熵合金由于其出色的機械性能和多樣化的微觀結構而受到了廣泛關注。然而,由于高熵合金設計空間的維度巨大,傳統的材料設計方法變得低效且昂貴,從而導致高熵合金的巨大潛力尚未充分實現。因此,理性設計策略對于在這一廣闊的設計空間內有效發現具有期望性能的高熵合金至關重要。
材料的原子間勢函數是對材料進行原子模擬的基礎。原子間勢函數的準確性也決定的原子模擬的精確度。目前高熵合金理性設計發展緩慢的原因之一就是眾多原子間勢函數的缺失。為了解決這一挑戰,美國馬里蘭大學李騰教授課題組提出了一種基于圖神經網絡機器學習通用策略的原子間勢函數的發展方案,旨在建立高熵合金中原子位置和原子力之間的復雜非線性關系,并以CrFeCoNiPd作為模型材料對這一發展方案進行了成功的展示。該方案獲得的機器學習模型可以在原子力方面實現顯著的預測精度(R2>0.92),且能夠準確模擬高熵合金材料的力學性能和變形機理。相關工作以“A machine learning interatomic potential for high entropy alloys” 為題,近期發表于國際力學領域旗艦期刊《Journal of the Mechanics and Physics of Solids》。
圖1 為基于圖神經網絡機器學習通用策略機器學習的原子間勢函數開發過程。通過頭分子動力學計算,獲得合金在不同溫度下原子的位置,能量,原子間的力和原子間的應力。提取原子位置信息,將位置信息和原子電負性作為機器模型的輸入,原子能量為輸出,對模型訓練。最后根據原子的能量,計算原子間的力獲得模型的力場信息。圖2對比了模型預測的原子能量以及原子間的力與頭分子動力學計算的原子能量以及原子間力,證實了模型具有很高的預測精度。

圖1: 基于圖神經網絡機器學習通用策略機器學習的原子間勢函數開發過程的示意圖。a, 生成訓練數據集;b, 構建機器學習模型;c, 計算原子力并組裝原子力場.
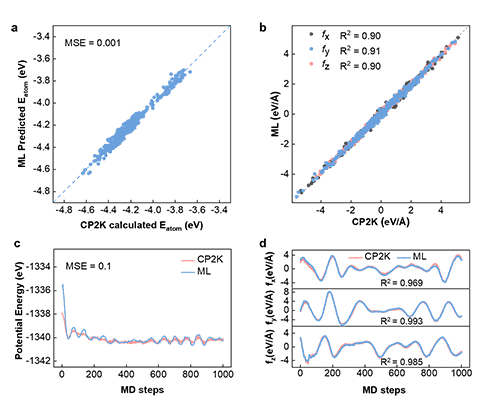
圖2: 機器學習模型評估:a-b 機器學習模型預測的原子能量和原子間力與頭分子動力學模擬計算結果對比;c-d 系統中第一個原子的原子力在300K下1000個動態演化過程的變化,與頭分子動力學模擬計算的結果比較。
為進一步驗證機器學習模型的準確性,李騰教授課題組將機器學習原子間勢函數嵌入LAMMPS軟件,然后進行蒙特卡羅分子動力學模擬,以獲得CrFeCoNiPd 合金的穩定結構。由圖3可以看出,在形成穩定結構的過程中,Pd原子有更明顯的聚合現象。最后,利用機器學習原子間勢函數預測的晶格常數及層錯能與實驗作對比如圖3d和圖3e所示,預測結果與實驗相近。這進一步證實了機器學習勢函數的準確性。
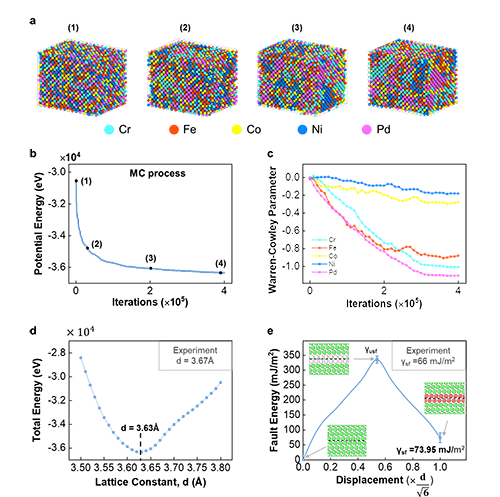
圖3: 機器學習原子間勢函數分析CrFeCoNiPd 高熵合金的原子結構 :a, MC模擬過程中原子結構; b, MC過程中能量變化; c, MC過程中WCP的變化; d, CrFeCoNiPd 高熵合金的晶格參數; e, 層錯錯能曲線。
為了證明本文發展的機器學習勢函數的應用性,李騰教授課題組利用機器學習原子間勢函數模擬了高熵合金 CrFeCoNiPd的壓縮過程,并首次通過系統的模擬揭示了壓縮過程中的變形機理其中包括位錯的形成,位錯的滑移及層錯的生成過程。壓縮模擬過程中發現的位錯交滑移現象與實驗觀察一致。這進一步證實了機器學習勢函數的實用性和準確性。模擬也揭示了高堆垛層錯能在改善CrFeCoNiPd 高熵合金強度中的關鍵作用。

圖4 基于機器學習原子間勢函數的CrFeCoNiPd 合金壓縮模擬。 a, 壓縮應力應變曲線及不同應變下的原子圖;b, 變形中的交滑移過程。
建立基于圖神經網絡機器學習通用策略的原子間勢函數的策略為推動高熵合金的路線設計帶來了新的思路,未來可能推動更高效和精確地探索更多新的高性能高熵合金。
論文鏈接:L Wu, T Li, A machine learning interatomic potential for high entropy alloys, Journal of the Mechanics and Physics of Solids, 105639 (2024)
https://doi.org/10.1016/j.jmps.2024.105639
