軟磁流變彈性體是一種在彈性基體中嵌入軟磁性粒子的智能材料。在磁場作用下，軟磁流變彈性體具有明顯的磁致變形行為，在軟體機器人、觸覺顯示等領域具有廣闊的應用前景。現(xiàn)有大多數(shù)關于軟磁流變彈性體的理論工作都集中在描述其準靜態(tài)力磁耦合行為上，而忽略了慣性對其力磁耦合行為的影響。然而，慣性對于軟磁流變彈性體在磁驅動領域的應用起著至關重要的作用。例如，當軟磁流變彈性體膜被外部磁場快速驅動時，它可能發(fā)生共振。此外，由于麥克斯韋力與磁通密度的平方成正比，軟磁流變彈性體可能發(fā)生超諧振動。除此之外，由于磁場的歐拉特性，施加在軟磁流變彈性體驅動器上的麥克斯韋力不僅取決于所施加的磁通密度，也和驅動器的結構變形有關。因此，基于軟磁流變彈性體的磁驅動系統(tǒng)實際上是一個參變系統(tǒng)。
為彌補軟磁流變彈性體驅動行為中慣性作用的缺失，中國科學技術大學龔興龍團隊提出了一種新型的，包含各向同性軟磁流變彈性體的磁化、非線性粘彈和慣性效應的力磁耦合動力學模型，以探索磁場、慣性和粘彈行為對其磁驅動動力學行為的影響，并開發(fā)了和模型對應的有限元用戶子單元程序，用于指導各向同性軟磁流變彈性體驅動器的設計和應用。相關研究成果以“Modelling the dynamic magnetic actuation of isotropic soft magnetorheological elastomers”發(fā)表在國際力學Top期刊International Journal of Mechanical Sciences上。論文的第一作者為中國科學技術大學工程科學學院博士后汪伯潮，通訊作者為龔興龍教授。
首先作者采用連續(xù)介質力學方法，建立了包含各向同性軟磁流變彈性體超彈、磁化和非線性粘彈行為的自由能函數(shù)，之后通過引入克勞修斯-普朗克不等式，得到了本構模型對應的應力和磁場強度表達。參數(shù)擬合之后，各向同性軟磁流變彈性體準靜態(tài)應力應變（圖1a）、磁化（圖1b）和在不同應變幅值/加載頻率下的粘彈性應力應變滯回曲線（圖1c）的實驗和模型結果的對比表明，所建立的模型能夠準確地刻畫各向同性軟磁流變彈性體的磁化和非線性粘彈力學行為。
圖1 各向同性軟磁流變彈性體的準靜態(tài)應力應變（a）、磁化（b）和非線性粘彈應力應變滯回曲線（c）實驗（Exp）和模擬（Sim）結果對比
隨后，作者將本構模型進行了有限元離散化，從而引入了慣性項的貢獻，并比較了力磁耦合平面應變四節(jié)點等參單元在簡單剪切強迫振動（圖2a）、靜態(tài)磁驅動（圖2b）和動態(tài)磁驅動（圖2c）下的理論解和有限元模擬解，驗證了力磁耦合動力學模型在有限元層面的正確編碼。有趣的是，對于正弦磁場激勵，由于麥克斯韋力與磁通密度的平方成正比，力磁耦合平面應變四節(jié)點等參單元的動態(tài)磁驅動行為表現(xiàn)出明顯的超諧振動特性。具體體現(xiàn)為系統(tǒng)的振動頻率是磁場激勵頻率的兩倍，見圖2c。
圖2 各向同性軟磁流變彈性體力磁耦合平面應變等參單元在簡單剪切強迫振動（a）、準靜態(tài)磁驅動（b）和動態(tài)磁驅動（c）下的理論解（Analytical）/數(shù)值解（Numerical）和有限元模擬解（FEM）的對比
之后，利用已驗證的力磁耦合單元，作者對由各向同性軟磁流變彈性體和非磁性彈性體組成的雙層梁的磁驅動動力學行為進行了有限元模擬。通過有限元仿真模擬，旨在了解慣性和粘彈性行為對各向同性軟磁流變彈性體磁致變形的影響，揭示各向同性軟磁流變彈性體驅動結構的非線性磁驅動行為和設計對應的磁場控制策略，并確保各向同性軟磁流變彈性體驅動器的磁驅動行為按照預期進行。
第一個有限元案例分析對應的力磁邊界條件和示意圖見圖3a，在該案例分析中，作者模擬了具有不同傾角的懸臂梁分別在采用超彈性、超彈和粘彈、超彈和粘彈及慣性材料模型下的磁致偏轉行為。毫無疑問，在施加磁場后，由于各向同性軟磁流變彈性體和不導磁彈性體層之間的應力失配，雙層梁會發(fā)生彎曲變形。圖3b的結果表明，不同傾角的雙層梁在同一磁場下的偏轉方向是不同的。對應的物理機制見圖3a。而具有不同傾角的雙層梁頂部中點沿x軸的位移見圖c。和其他兩種材料模型相比，施加給定磁通密度時，只包含超彈行為的材料模型對應的磁致變形最大。其原因在于慣性和粘彈性行為在一定程度上阻礙了材料的磁致變形行為，但同時，慣性和粘彈性也延緩了有限元仿真模擬中的數(shù)值不收斂行為。除此之外，圖3c中的子圖的結果表明，對于具有零度傾斜角和采用動態(tài)粘彈材料模型的雙層梁，在磁場激勵后，會出現(xiàn)輕微的振蕩現(xiàn)象。
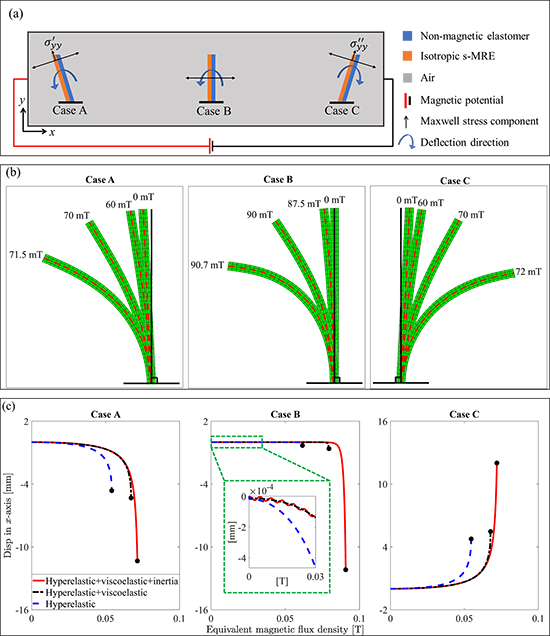
圖3 具有不同傾角的各向同性軟磁流變彈性體雙層懸臂梁（a）在磁場激勵下產(chǎn)生的麥克斯韋力、對應的磁致偏轉（b）以及采用不同材料模型梁磁致位移的比較（c），有限元數(shù)值不收斂的開始通過圖中的圓點符號表示
第二個有限元案例分析涉及各向同性軟磁流變彈性體和不導磁彈性體雙層固支梁在動態(tài)磁場激勵下的磁驅動力響應，固支梁的磁場邊界條件和磁驅動變形分別見圖4a和b。盡管簡化的固支梁結構和實際的磁驅動結構存在差異，但通過這種磁驅動二維雙層固支梁的有限元案例分析可揭示磁驅動結構內(nèi)在復雜的非線性動力學行為。首先對固支梁施加幅值為0.05 T的正弦交變磁場，雙層梁上部中點沿y軸的峰值位移、谷值位移和峰谷值位移和磁場激勵頻率的關系如圖5a所示。三個代表性頻率下的變形時間歷程、FFT變換結果、相圖和龐加萊圖如圖5b至5g所示。由于磁致激勵力與磁通密度的平方成正比，梁的振動體現(xiàn)出超諧振動行為。該仿真模擬結果表明，基于各向同性軟磁流變彈性體磁驅動系統(tǒng)的高頻振動可以通過施加相對低頻的磁場激勵信號產(chǎn)生。由于信號的衰減隨頻率的增加而增大，這種機制可以提高能量和信息的傳輸效率。此外，對于各向同性軟磁流變彈性體驅動系統(tǒng)在柔性運動機器人領域的應用而言，可以利用這種共振機制放大驅動器的位移，從而降低對應所需的驅動磁場功率。值得注意的是，為了使系統(tǒng)達到這樣的諧振放大振蕩，磁場激勵頻率應該是系統(tǒng)諧振頻率的一半。
圖4各向同性軟磁流變彈性體雙層固支梁（a）在磁場激勵下的磁致變形行為（b），對應的磁通密度為0.1 T
圖5各向同性軟磁流變彈性體雙層固支梁沿y軸位移和磁場激勵頻率的關系（a），（a）中三個典型磁驅動頻率下對應的位移時程結果、FFT變換結果、相圖和龐加萊圖分別列于（b）、（c）、（d）、（e）、（f）、（g）中，圖（b）、（c）、（d）中的菱形符號對應磁場激勵的頻率
隨后，作者進行了固支梁在不同磁通密度正弦交變磁場下磁驅動行為的模擬，結果見圖6a。顯然，固支梁存在著雙穩(wěn)態(tài)共振行為。以0.07 T磁通密度為例，當磁場激勵頻率超過第二階共振頻率（9.15 Hz）時，位移急劇減小。為判斷第二階共振頻率是否對應非線性動力系統(tǒng)中的共振跳躍行為，作者對固支梁施加了從7.5 Hz到11.5 Hz的正向和反向掃頻磁場激勵，對應的位移時程結果見圖6b，顯然，在正向和反向掃頻磁場激勵下雙層梁的峰值位移是完全不同的。這種共振跳躍行為可歸因于所施加磁場的歐拉性質，以及慣性和麥克斯韋力之間的復雜耦合作用。另一方面，如圖6a所示，固支梁的共振頻率隨著所施加磁通密度的增大而減小。這背后的物理機制為：對于正弦磁場激勵而言，較大的磁通密度對應較大的靜態(tài)麥克斯韋力。較大的靜態(tài)麥克斯韋力使得梁產(chǎn)生較大的初始彎曲，從而降低了系統(tǒng)的整體剛度。因此，固支梁的共振頻率在高磁通密度下反而有所降低。
圖6（a）雙層固支梁在不同磁通密度下的峰谷值位移和磁場加載頻率的關系; （b）雙層梁在正向和反向正弦磁場掃頻激勵下的位移時程結果
上述仿真分析案例結果表明，基于各向同性軟磁流變彈性體驅動器的磁驅動響應可以通過調(diào)節(jié)施加的磁場激勵來進行調(diào)控。為此，作者提出了用于調(diào)諧雙層梁振動頻率的磁場激勵調(diào)控策略。具體而言，對于包含恒定和交變分量混合磁場的各向同性軟磁流變彈性體固支梁而言，利用麥克斯韋力和磁通密度平方成正比的特點，固支梁的振動頻率可通過改變恒定磁場的大小來調(diào)節(jié)，而無需改變對應交變磁場的頻率，相關模擬結果見圖7。在該有限元案例分析中，交變磁場的激勵頻率設置為4 Hz。在第一階段，僅對固支梁施加交變磁場激勵，對應的穩(wěn)態(tài)位移時程結果、FFT變換結果、相圖和龐加萊圖如圖7b和7e所示。由于激勵力與所施加磁通密度的平方成正比，第一階段系統(tǒng)的主振動頻率為8 Hz。在第二階段，作者在第一階段基礎上添加了幅值為交變磁場四倍的恒定磁場激勵，相應的穩(wěn)態(tài)位移時程結果、傅里葉變換結果、相圖和龐加萊圖見圖7c和7f。由于交變/恒定磁場比例很小，該階段系統(tǒng)的主振動頻率從8 Hz降低到4 Hz，表現(xiàn)出輕微的諧波失真行為（見7c中的位移傅里葉變換結果和7f中的相圖）。在第三階段，將恒定磁場的比例減小到第二階段的一半，相應的穩(wěn)態(tài)位移時程結果、傅里葉變換結果、相圖和龐加萊圖見圖7d和7g？梢钥吹，此階段位移響應中出現(xiàn)了三個諧波分量。由此可見，相較于傳統(tǒng)的線性動態(tài)系統(tǒng)，基于各向同性軟磁流變彈性體的磁驅動系統(tǒng)，動力學行為復雜多變。驅動器的位移響應不僅取決于所施加交變磁場的頻率，還和恒定磁場與交變磁場之間的振幅比密切相關。
圖7（a）磁通密度和雙層梁位移隨時間的變化（a）以及不同磁場激勵條件下的穩(wěn)態(tài)位移時程結果、傅里葉變換結果、對應的相圖和龐加萊圖（b）、（c）、（d）、（e）、（f）、（g），圖中的菱形符號對應交變磁場激勵的頻率
本研究建立了一種新型的，反映各向同性軟磁流變彈性體力磁耦合動力學行為的本構模型。在驗證了該模型在有限元層面上的正確編碼后，本研究通過有限元案例分析深入研究了由各向同性軟磁流變彈性體和不導磁彈性體組成的雙層懸臂梁的磁驅動動力學行為，揭示了慣性和粘彈性對各向同性軟磁流變彈性體磁驅動器的磁驅動變形行為的影響。此外，該研究還分析了由各向同性軟磁流變彈性體和不導磁彈性體組成的雙層固支梁在磁場激勵下的磁驅動相應。研究揭示了由麥克斯韋力和外加磁場強度之間的平方比關系，以及磁場的歐拉性質所導致的各向同性軟磁流變彈性體磁驅動器的超諧振動和共振跳躍等非線性振動現(xiàn)象。此外，案例分析結果表明，改變直流磁場和交變磁場之間的比例可以實現(xiàn)對各向同性軟磁流變彈性體磁驅動器動力學行為靈活地調(diào)整。這些發(fā)現(xiàn)大大促進了對軟磁流變彈性動態(tài)行為的理解，為軟磁流變彈性在磁場驅動領域的實際應用鋪平了道路。
原文鏈接：Bochao Wang, Leif Kari, Haoming Pang, Xinglong Gong. Modelling the dynamic magnetic actuation of isotropic soft magnetorheological elastomers, International Journal of Mechanical Sciences, 2023: 108908
https://doi.org/10.1016/j.ijmecsci.2023.108908
